|
DOCENTE |
Michele
Picotti |
|
|
|
|
|
|
Materia |
Matematica |
Classe |
5Bp |
A.S. 2007/2008 |
||
Programma di
matematica
·
Definizione di
funzione e dominio.
·
Concetto di
limite e definizioni relative ad ogni caso.
·
Calcolo dei limiti
e forme indeterminate.
·
Limite delle somma e del prodotto di funzioni (con dimostrazione).
·
Definizione di
funzione continua.
·
Discontinuità di
1°, 2° 3° specie.
·
Asintoti
verticali, orizzontali e obliqui.
·
Definizione di
rapporto incrementale, di derivata e relativo significato geometrico.
·
Calcolo delle
derivate di alcune funzioni elementari come limite del
rapporto incrementale.
·
Teoremi sul
calcolo delle derivate: derivata della somma (dimostrazione), del prodotto (dimostrazione), del quoziente.
Regole di derivazione.
·
Continuità delle
funzioni derivabili (dimostrazione).
·
Equazione della
tangente in un punto al grafico di una funzione.
·
Teoremi di Rolle (dimostrazione) e Lagrange
(dimostrazione).
·
Massimi
e minimi, funzioni crescenti e decrescenti e uso della derivata prima.
·
Funzioni
concave e convesse, punti di flesso e uso della derivata seconda.
·
Teoremi di De
L'Hospital.
·
Studio e
rappresentazione delle funzione razionali e irrazionali
e semplici funzioni logaritmiche ed esponenziali
Testo
in adozione: M. Re Fraschini – G. Grazzi,
Moduli.Mat A1
Analisi, Atlas, Bergamo, 2001
Il docente
Michele
Picotti
Verona,
06 giugno 2008
1° - SIMULAZIONE TERZA PROVA
17
marzo 2008
Quesito
no1
a) Considerare una funzione di equazione
, definita in 
, scrivere la definizione di funzione continua in un punto di
ascissa c, con c interno all’intervallo.
b) Data la funzione di equazione
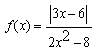
studiare
la continuità.
Quesito
no2
a) Cosa rappresenta geometricamente la derivata della
funzione , in un punto c del suo dominio?
b)
Data la
funzione f(x) =
, determinare la derivata nel punto di ascissa
xo
= -1.
2° - SIMULAZIONE TERZA PROVA
6 maggio 2008
1.
1. Calcola la derivata della funzione 
2. Determinare l’equazione della retta tangente alla
funzione nel suo punto di
ascissa 
.
2.
Studia continuità e derivabilità
della seguente funzione:
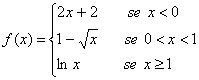
3.
1. Scrivi l’enunciato del teorema di Rolle.
2. Fornisci graficamente almeno tre esempi per far vedere che il teorema non è valido se viene meno una qualsiasi delle ipotesi.